Números Reais: Uma Exploração Detalhada: Através De Exemplos Indique Três Números Reais Diferentes Que Possuam
Através De Exemplos Indique Três Números Reais Diferentes Que Possuam – Os números reais formam a base de grande parte da matemática que utilizamos no dia a dia, desde cálculos simples até conceitos avançados de cálculo e geometria. Compreender sua natureza e propriedades é fundamental para diversas áreas do conhecimento.
Números Reais: Conceitos Fundamentais
Os números reais englobam todos os números que podem ser representados em uma reta numérica, incluindo números racionais (que podem ser expressos como uma fração de dois inteiros) e números irracionais (que não podem ser expressos como uma fração de dois inteiros). Suas principais características incluem a densidade (entre quaisquer dois números reais, existe um infinito de outros números reais) e a completude (toda sequência de Cauchy de números reais converge para um número real).
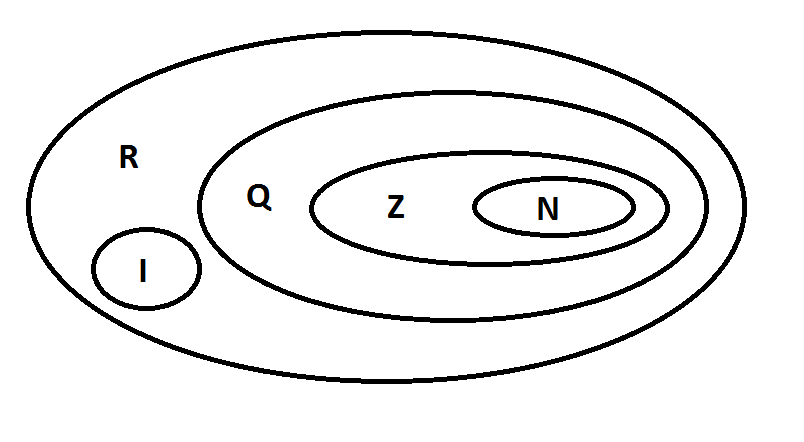
Os números reais se diferenciam dos números naturais (1, 2, 3…), inteiros (…,-2, -1, 0, 1, 2…) e racionais (frações de inteiros) pela inclusão dos números irracionais, como π (pi) e √2 (raiz quadrada de 2). Os números naturais são um subconjunto dos inteiros, que por sua vez são um subconjunto dos racionais, e os racionais e irracionais juntos formam os reais.
A representação na reta real é visual: cada número real corresponde a um ponto único na reta. Observe a tabela abaixo para exemplos.
| Número | Tipo | Representação Decimal | Posição na Reta Real |
|---|---|---|---|
| 2 | Racional | 2.00000 | Dois unidades à direita da origem. |
| -1/2 | Racional | -0.50000 | Meia unidade à esquerda da origem. |
| √3 | Irracional | 1.73205… | Entre 1 e 2, mais próximo de 2. |
Exemplos de Números Reais Diferentes
Para ilustrar a diversidade dos números reais, escolhemos três exemplos distintos: um racional positivo, um racional negativo e um irracional.
- 2,5: Número racional positivo. Sua representação fracionária é 5/2.
- -0,75: Número racional negativo. Sua representação fracionária é -3/4.
- π/2 ≈ 1,5707963: Número irracional. π (pi) é uma constante matemática que representa a razão entre o comprimento de uma circunferência e seu diâmetro. Sua representação decimal é infinita e não periódica.
Propriedades dos Números Reais Selecionados, Através De Exemplos Indique Três Números Reais Diferentes Que Possuam

A comparação entre os números 2,5, -0,75 e π/2 revela diferenças significativas em suas representações decimais e posições na reta numérica. 2,5 é um número inteiro e meio, -0,75 é negativo e π/2 é um irracional situado entre 1 e 2.
As operações aritméticas básicas entre pares desses números são:
| Operação | Resultado |
|---|---|
| 2,5 + (-0,75) | 1,75 |
| 2,5 – π/2 | ≈ 0,9292 |
| 2,5 – (-0,75) | -1,875 |
| 2,5 / π/2 | ≈ 1,5915 |
Representação Gráfica e Interpretação

Na reta numérica, 2,5 estaria localizado 2,5 unidades à direita da origem. -0,75 estaria localizado 0,75 unidades à esquerda da origem. π/2 estaria localizado aproximadamente 1,57 unidades à direita da origem, entre 1 e 2, mais próximo de 2.
A relação de ordem entre os três números é: -0,75 < π/2 < 2,5. A imagem mental da reta numérica mostra três pontos distintos, claramente espaçados de acordo com seus valores. A escala seria ajustada para acomodar o intervalo que inclui esses três números, com uma precisão suficiente para distinguir a posição de cada um.
Aplicações dos Números Reais
Os números reais são amplamente utilizados em diversas situações do cotidiano:
- Medição de temperatura: A temperatura de um ambiente pode ser representada por um número real, como 25,5°C. O número real indica a precisão da medição.
- Cálculo de área: A área de um círculo, dada pela fórmula πr², utiliza o número irracional π para calcular a área com precisão.
- Balanço financeiro: Um saldo bancário de -R$150,00 é um número real negativo que representa um débito.
Em resumo, exploramos a riqueza e a diversidade dos números reais através de exemplos práticos e detalhados. Observamos a distinção entre números racionais e irracionais, suas representações decimais e suas posições na reta real. Compreender as operações aritméticas entre esses números e suas aplicações no mundo real é crucial para fortalecer o conhecimento matemático. Esperamos que esta análise tenha contribuído para uma compreensão mais clara e abrangente dos números reais, destacando sua importância em diversas áreas do conhecimento e da vida cotidiana.
A jornada pela matemática continua, e a exploração de conceitos como os números reais é uma etapa essencial nesse caminho.

